Eksponencijalna raspodela

Eksponencijalna
Funkcija gustine verovatnoće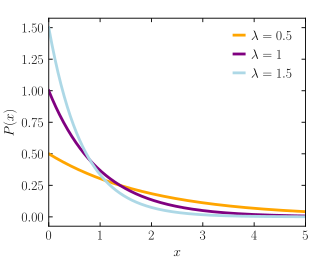
Grafički prikaz funkcije gustine verovatnoće eksponencijalne distribucije plot of the probability density function of the exponential distribution
Funkcija kumulativne raspodele
Funkcija kumulativne distribucije
Parametriλ > 0 stopa, ili inverzna skala
Nositeljx ∈ [0, ∞)
PDFλ e−λx
CDF1 − e−λx
Kvantil−ln(1 − F) / λ
Prosekλ−1 (= β)
Medijanaλ−1ln(2)
Modus0
Varijansaλ−2 (= β2)
Koef. asimetrije2
Kurtoza6
Entropija1 − ln(λ)
MGF λ λ − t ,  for  t < λ {\displaystyle {\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda }
CF λ λ − i t {\displaystyle {\frac {\lambda }{\lambda -it}}}
Fišerova informacija λ − 2 {\displaystyle \lambda ^{-2}}
Kulbek-Lajblerova divergencija D K L ( exp 0 ∥ exp 1 ) = log ⁡ ( λ 0 ) − log ⁡ ( λ ) + λ λ 0 − 1 {\displaystyle D_{KL}(\exp _{0}\parallel \exp _{1})=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1}

U teoriji verovatnoće i statistici, eksponencijalna raspodela (pozanta kao negativna eksponencijalna raspodela) je raspodela verovatnoće vremena između događaja u Poasonovom procesu,[1][2] i.e., procesu u kome se događaji kontinuirano i nezavisno javljaju sa konstantnom prosečnom brzinom. To je poseban slučaj gama distribucije. Eksponencijalna distribucija je kontinuirani analog geometrijske distribucije i ima ključno svojstvo da je bez memorije. Pored toga što se koristi za analizu Poasonovih tačkastih procesa, ona se javlja u mnoštvu drugih konteksta.

Eksponencijalna distribucija nije isto što i klasa eksponencijalne familije distribucija, koja je velika klasa distribucija verovatnoće kojom je obuhvaćena eksponencijalna distribucija kao jedan od njenih članova, ali takođe uključuje normalnu distribuciju, binomnu distribuciju, gama distribuciju, Poasonovu, i mnoge druge.

Karakterizacija

Funkcija gustine verovatnoće

Funkcija gustine verovatnoće eksponencijalne distribucije je

f ( x ; λ ) = { λ e − λ x x ≥ 0 , 0 x < 0. {\displaystyle f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}

Alternativno, ovo se može definisati korišćenjem desne-kontinuirane Hevisajdove odskočne funkcije, H(x) gde je H(0) = 1:[3][4]

f ( x ; λ ) = λ e − λ x H ( x ) {\displaystyle f(x;\lambda )=\lambda e^{-\lambda x}H(x)}

Ovde je λ > 0 parameter distribucije, koji se obično naziva parametar brzine. Distribucija je podržana na intervalu [0, ∞). Ako slučajna promenljiva X ima ovu distribuciju, piše se X ~ Exp(λ).

Eksponencijalna distribucija ispoljava beskonačnu deljivost.

Funkcija kumulativne distribucije

Funkcija kumulativne distribucije je data sa

F ( x ; λ ) = { 1 − e − λ x x ≥ 0 , 0 x < 0. {\displaystyle F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}

Alternativno, ovo se može definisati koristeći Hevisajdovu odskočnu funkciju, H(x).

F ( x ; λ ) = ( 1 − e − λ x ) H ( x ) {\displaystyle F(x;\lambda )=\mathrm {(} 1-e^{-\lambda x})H(x)}

Alternativna parametrizacija

Najčešće korišćena alternativna parametrizacija je putem definisanja funkcije gustine verovatnoće (pdf) eksponencijalne distribucije kao što je

f ( x ; β ) = { 1 β e − x β x ≥ 0 , 0 x < 0. {\displaystyle f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-{\frac {x}{\beta }}}&x\geq 0,\\0&x<0.\end{cases}}}

gde je β > 0 srednja vrednost, standardna devijacija, i parametar skale distribucije, recipročna vrednost parametra brzine, λ, definisanog iznad. U ovoj specifikaciji, β je parametar preživljavanja u smislu da ako je slučajna varijabla X vremensko trajanje tokom koga određeni biološki ili mehanički sistem uspe da preživi i X ~ Exp(β), onda je E[X] = β. Naime, očekivano trajanje preživljavanja sistema je β jedinica vremena. Parametrizacija koja uključuje parametar „brzine” nastaje u kontekstu događaja koji pristižu brzinom λ, kada vreme između događaja (koje se može modelovati koristeći eksponencijalnu distribuciju) ima srednju vrednost β = λ−1.

Alternativna specifikacija je ponekad podesnija od gore navedene, a neki autori je koriste kao standardnu definiciju. Ova alternativna specifikacija se ovde ne koristi. Nažalost, to dovodi do nejasnoća u notacijama. Generalno, čitalac mora proveriti koja se od ove dve specifikacije koristi, ako autor piše „X ~ Exp(λ)”, misli se bilo na notaciju iz prethodne sekcije (koristeći λ) ili na notaciju iz ove sekcije (ovde, koristeći β da se izegne zabuna).[5]

Osobine

Srednja vrednost, varijansa, momenti i medijana

Srednja vrednost je centar mase verovatnoće, odnosno prvi momenat.
Medijana je praslikavanje F−1(1/2).

Srednja ili očekivana vrednost eksponencijalno raspoređene slučajne promenljive X sa parametrom brzine λ je data sa

E ⁡ [ X ] = 1 λ . {\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}.}

U svetlu dole navedenih primera, ovo ima smisla: ako se primaju telefonski pozivi u proseku dva puta na sat, onda se može očekivati da će se čekati pola sata na svaki poziv.

Varijanca od X je data sa

Var ⁡ [ X ] = 1 λ 2 , {\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},}
tako da je standardna devijacija jednaka sa srednjom vrednošću.

Momenti od X, za n ∈ N {\displaystyle n\in \mathbb {N} } su dati sa

E ⁡ [ X n ] = n ! λ n . {\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.}

Centralni momenti od X, za n ∈ N {\displaystyle n\in \mathbb {N} } su dati sa

μ n = ! n λ n = n ! λ n ∑ k = 0 n ( − 1 ) k k ! . {\displaystyle \mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.}

gde je !n podfaktorijal od n

Medijana od X je data sa

m ⁡ [ X ] = ln ⁡ ( 2 ) λ < E ⁡ [ X ] , {\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],}
gde se ln odnosi na prirodni logaritam. Stoga je apsolutna razlika između srednje vrednosti i medijane
| E ⁡ [ X ] − m ⁡ [ X ] | = 1 − ln ⁡ ( 2 ) λ < 1 λ = σ ⁡ [ X ] , {\displaystyle \left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],}

u skladu sa srednjom vrednosti nejednakost.

Svojstvo nepamćenja eksponencijalne slučajne promenljive

Eksponencijalno raspoređena slučajna promenljiva T poštuje odnos

Pr ( T > s + t ∣ T > s ) = Pr ( T > t ) , ∀ s , t ≥ 0. {\displaystyle \Pr \left(T>s+t\mid T>s\right)=\Pr(T>t),\qquad \forall s,t\geq 0.}

Ovo se može videti ako se uzme u obzir komplementarna kumulativna funkcija distribucije:

Pr ( T > s + t ∣ T > s ) = Pr ( T > s + t ∩ T > s ) Pr ( T > s ) = Pr ( T > s + t ) Pr ( T > s ) = e − λ ( s + t ) e − λ s = e − λ t = Pr ( T > t ) . {\displaystyle {\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}}

Kada se T tumači kao vreme čekanja da se događaj desi u odnosu na neko početno vreme, ova relacija implicira da, ako je T uslovljeno neuspehom da se posmatra događaj tokom nekog početnog vremenskog perioda s, distribucija preostalog vremena čekanja je isto što i originalna bezuslovna raspodela. Na primer, ako se događaj nije dogodio nakon 30 sekundi, uslovna verovatnoća da će za događaj biti potrebno još najmanje 10 sekundi jednaka je bezuslovnoj verovatnoći posmatranja događaja više od 10 sekundi nakon početnog vremena.

Eksponencijalna raspodela i geometrijska raspodela su jedine raspodele verovatnoće bez memorije.

Eksponencijalna raspodela je stoga nužno i jedina kontinuirana raspodela verovatnoće koja ima konstantnu stopu neuspeha.

Kvantili

Tukey anomaly criteria for exponential probability distribution function.
Tukijevi kriterijumi za anomalije.

Funkcija kvantila (inverzna kumulativna funkcija raspodele) za Exp(λ) je

F − 1 ( p ; λ ) = − ln ⁡ ( 1 − p ) λ , 0 ≤ p < 1 {\displaystyle F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1}

Prema tome, kvartili su:

  • prvi kvartil: ln(4/3)/λ
  • medijana: ln(2)/λ
  • treći kvartil: ln(4)/λ

Kao posledica toga, interkvartilni opseg je ln(3)/λ.

Uslovna vrednost pod rizikom (očekivani nedostatak)

Uslovna vrednost pod rizikom (CVaR) takođe poznata kao očekivani nedostatak ili superkvantil za Exp(λ) se izvodi na sledeći način:[6]

q ¯ α ( X ) = 1 1 − α ∫ α 1 q p ( X ) d p = 1 ( 1 − α ) ∫ α 1 − ln ⁡ ( 1 − p ) λ d p = − 1 λ ( 1 − α ) ∫ 1 − α 0 − ln ⁡ ( y ) d y = − 1 λ ( 1 − α ) ∫ 0 1 − α ln ⁡ ( y ) d y = − 1 λ ( 1 − α ) [ ( 1 − α ) ln ⁡ ( 1 − α ) − ( 1 − α ) ] = − ln ⁡ ( 1 − α ) + 1 λ {\displaystyle {\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}}

Buferovana verovatnoća prekoračenja (bPOE)

Baferovana verovatnoća prekoračenja je jedan minus nivo verovatnoće na kome je CVaR jednak pragu x {\displaystyle x} . Izvodi se na sledeći način:[6]

p ¯ x ( X ) = { 1 − α | q ¯ α ( X ) = x } = { 1 − α | − ln ⁡ ( 1 − α ) + 1 λ = x } = { 1 − α | ln ⁡ ( 1 − α ) = 1 − λ x } = { 1 − α | e ln ⁡ ( 1 − α ) = e 1 − λ x } = { 1 − α | 1 − α = e 1 − λ x } = e 1 − λ x {\displaystyle {\begin{aligned}{\bar {p}}_{x}(X)&=\{1-\alpha |{\bar {q}}_{\alpha }(X)=x\}\\&=\{1-\alpha |{\frac {-\ln(1-\alpha )+1}{\lambda }}=x\}\\&=\{1-\alpha |\ln(1-\alpha )=1-\lambda x\}\\&=\{1-\alpha |e^{\ln(1-\alpha )}=e^{1-\lambda x}\}=\{1-\alpha |1-\alpha =e^{1-\lambda x}\}=e^{1-\lambda x}\end{aligned}}}

Kulback–Liblerova divergencija

Usmerena Kulbak–Liblerova divergencija u natima od e λ {\displaystyle e^{\lambda }} („približna“ distribucija) od e λ 0 {\displaystyle e^{\lambda _{0}}} („prava“ distribucija) daje

Δ ( λ 0 ∥ λ ) = E λ 0 ( log ⁡ p λ 0 ( x ) p λ ( x ) ) = E λ 0 ( log ⁡ λ 0 e λ 0 x λ e λ x ) = log ⁡ ( λ 0 ) − log ⁡ ( λ ) − ( λ 0 − λ ) E λ 0 ( x ) = log ⁡ ( λ 0 ) − log ⁡ ( λ ) + λ λ 0 − 1. {\displaystyle {\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}}

Maksimalna raspodela entropije

Među svim kontinuiranim raspodelama verovatnoće sa podrškom na [0, ∞) i srednjom vrednošću μ, eksponencijalna raspodela sa λ = 1/μ ima najveću diferencijalnu entropiju. Drugim rečima, to je maksimalna distribucija verovatnoće entropije za slučajnu promenljivu X koja je veća ili jednaka nuli i za koju je E[X] fiksno.[7]

Reference

  1. ^ Stirzaker, David (2000). „Advice to Hedgehogs, or, Constants Can Vary”. The Mathematical Gazette. 84 (500): 197—210. ISSN 0025-5572. JSTOR 3621649. doi:10.2307/3621649. 
  2. ^ Guttorp, Peter; Thorarinsdottir, Thordis L. (2012). „What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes”. International Statistical Review. 80 (2): 253—268. ISSN 0306-7734. doi:10.1111/j.1751-5823.2012.00181.x. 
  3. ^ Calvert, James B. (2002). „Heaviside, Laplace, and the Inversion Integral”. University of Denver. 
  4. ^ Davies, Brian (2002). „Heaviside step function”. Integral Transforms and their Applications (3rd изд.). Springer. стр. 28. 
  5. ^ David Olive, Chapter 4. Truncated Distributions, "Lemma 4.3", Southern Illinois University, February 18, 2010, pp. 107.
  6. ^ а б Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). „Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation” (PDF). Annals of Operations Research. Springer. 299 (1-2): 1281—1315. doi:10.1007/s10479-019-03373-1. Архивирано из оригинала (PDF) 31. 03. 2023. г. Приступљено 2023-02-27. 
  7. ^ Park, Sung Y.; Bera, Anil K. (2009). „Maximum entropy autoregressive conditional heteroskedasticity model” (PDF). Journal of Econometrics. Elsevier. 150 (2): 219—230. doi:10.1016/j.jeconom.2008.12.014. Архивирано из оригинала (PDF) 2016-03-07. г. Приступљено 2011-06-02. 

Literatura

  • B. S. Everitt (2006). The Cambridge Dictionary of Statistics (3rd изд.). Cambridge: Cambridge University Press. ISBN 978-0-521-69027-0. 
  • Bishop (2006). Pattern Recognition and Machine Learning. Springer. ISBN 978-0-387-31073-2. 
  • den Dekker, A. J.; Sijbers, J. (2014). „Data distributions in magnetic resonance images: A review”. Physica Medica. 30 (7): 725—741. PMID 25059432. doi:10.1016/j.ejmp.2014.05.002. 
  • Sung Nok Chiu; Stoyan, Dietrich; Wilfrid S. Kendall; Mecke, Joseph (27. 6. 2013). Stochastic Geometry and Its Applications. John Wiley & Sons. ISBN 978-1-118-65825-3. 
  • J. F. C. Kingman (17. 12. 1992). Poisson Processes. Clarendon Press. ISBN 978-0-19-159124-2. 
  • Pierre Simon de Laplace (1812). Analytical Theory of Probability. 
  • A. Kolmogoroff (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung. ISBN 978-3-642-49888-6. doi:10.1007/978-3-642-49888-6. 
  • Billingsley, Patrick (1979). Probability and Measure. New York, Toronto, London: John Wiley and Sons. 
  • Olav Kallenberg; Foundations of Modern Probability, Springer Series in Statistics.. 650 pp. (2nd изд.). 2002. ISBN 978-0-387-95313-7. 
  • Tijms, Henk (2004). Understanding Probability. Cambridge University Press. 
  • Olav Kallenberg; Probabilistic Symmetries and Invariance Principles. Springer -Verlag, New York. 510 pp. 2005. ISBN 978-0-387-25115-8.
  • Gut, Allan (2005). Probability: A Graduate Course. Springer-Verlag. ISBN 978-0-387-22833-4. 

Spoljašnje veze

Eksponencijalna raspodela na Vikimedijinoj ostavi.
  • Hazewinkel Michiel, ур. (2001). „Exponential distribution”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
  • Online calculator of Exponential Distribution
Normativna kontrola: Državne Уреди на Википодацима
  • Nemačka