Spline

En spline er i matematikk en funksjon definert stykkevis av polynom.

Innen data, databasert design og datagrafikk refererer spline til en delvis parametrisk polynomfunksjon. Innen disse feltene er spline en populær måte å representere kurver på, på grunn av dens enkle konstruksjon, som likevel gir mulighet å gjennomføre komplekse en design ved hjelp av kurvetilpassing.

Terminologien spline kommer fra utstyr brukt av skipsbyggere og tegnere for å tegne glatte og jevne former. Utstyret var et langt stivt bånd festet på forskjellige punkter for å gi en ønsket form.

Typer spline:

• B-spline
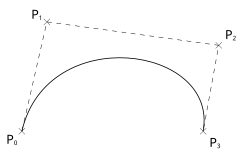
• Bezier-kurve
• Bezier-spline
• Hermite-spline
• Kubisk spline
• Naturlig spline
• Periodisk spline

Definisjon

Spline

Spline er en funksjon:

${\displaystyle S(t):[a,b]\rightarrow \mathbb {R} }$

består stykkevis av polynomer:

${\displaystyle P_{i}(t):[t_{i},t_{i+1})\rightarrow \mathbb {R} }$

hvor

${\displaystyle a=t_{0}<t_{1}<...<t_{k-2}<t_{k-1}=b\mathbb {} }$

og vi får splinefunksjonen

${\displaystyle S(t)={\begin{cases}P_{0}(t)\quad &,\quad t_{0}\leq t<t_{1}\\P_{1}(t)\quad &,\quad t_{1}\leq t<t_{2}\\\quad ...&,\quad ...\\P_{k-2}(t)\quad &,\quad t_{k-2}\leq t<t_{k-1}\end{cases}}}$

Skjøter

Alle de ${\displaystyle k}$ skjøtene ${\displaystyle t_{i}}$ (også kalt knutene) samles i en skjøtevektor

${\displaystyle {\vec {t}}=(t_{0},t_{1},...,t_{k-1})}$

Hvis avstanden mellom skjøtene er spredd jevnt i intervallet ${\displaystyle [a,b]}$, sier vi at splinen er uniform, ellers ikke-uniform.

Splinens grad

Hvis alle polynomene ${\displaystyle P_{i}}$ har grad n, sier vi at splinen er av grad ${\displaystyle \leq n}$

Glatthet ${\displaystyle C^{r_{i}}}$ og glatthetsvektor

Hvis ${\displaystyle S(t)\in C^{r_{i}}}$ befinner seg i nabolaget til ${\displaystyle t_{i}}$, sies splinen å være av glatthet (minst) ${\displaystyle C^{r_{i}}}$ ved ${\displaystyle t_{i}}$. Dette betyr at de to delene ${\displaystyle \{P_{i-1},P_{1}\}}$ deler felles deriverte fra orden null (funksjonsverdi) og opp til orden ${\displaystyle r_{i}}$.

Vektoren

${\displaystyle {\vec {r}}=(r_{1},r_{2},...,r_{k-2})}$

er slik at splinen har glatthet ${\displaystyle C^{r_{i}}}$ ved ${\displaystyle t_{i}}$ for ${\displaystyle 0<i<k-1}$, og kalles splinens glatthetsvektor.

Eksempler

Anta at intervallet [a,b] er [0,3], og delintervallene er [0,1), [1,2), og [2,3]. Anta at de stykkvise polynomene er av grad 2, og stykkene [0,1) og [1,2) må møtes i verdi og 1.derivert. (her må de altså møtes ved t=1). Stykkene [1,2) og [2,3) møtes i verdi t=2 .

Dette definere en type spline ${\displaystyle S(t)}$ hvor

${\displaystyle S(t)={\begin{cases}P_{0}(t)=-1+4t-t^{2}&{\mbox{ , }}0\leq t<1\\P_{1}(t)=2t&{\mbox{ , }}1\leq t<2\\P_{2}(t)=2-t+t^{2}&{\mbox{ , }}2\leq t\leq 3\end{cases}}}$

vil være medlem av den typen, og

${\displaystyle S(t)={\begin{cases}P_{0}(t)=-2-2t^{2}&{\mbox{ , }}0\leq t<1\\P_{1}(t)=1-6t+t^{2}&{\mbox{ , }}1\leq t<2\\P_{2}(t)=-1+t-2t^{2}&{\mbox{ , }}2\leq t\leq 3\end{cases}}}$

vil også være medlem av typen.

(Polynomet ${\displaystyle 2t}$ er fortsatt av andre grad fordi det kan skrives ${\displaystyle 0+2t+0t^{2}}$)

Skjøtvektoren til denne typen av spline er her

${\displaystyle {\vec {t}}=(0,1,2,3)}$

Den enkleste splinen har grad 0, og den er en stegfunksjon.

Den nest enkleste splinen har grad 1, og er også kalt en lineær spline.

En vanlig brukt spline er den naturlige kubiske spline som har grad 3 og kontinuitet ${\displaystyle C^{2}}$. Naturlig betyr i denne sammenhengen at splinen velges slik at den andrederiverte av splinepolynomene er null på endepunktene av interpoleringens intervall

${\displaystyle S''(a)\,=S''(b)=0}$.

Dette tvinger splinen til å være en rett linje utenfor intervallet og at kurven alle steder er glatt.

Eksterne lenker

• 40 år med algoritmen du ikke vet om, men som alle bruker Arkivert 27. september 2019 hos Wayback Machine.