Polarkoordinatsystem

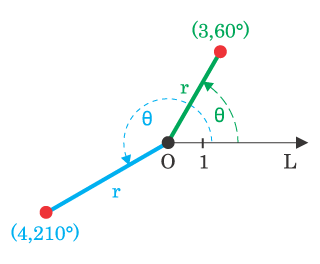
Et polarkoordinatsystem er et koordinatsystem hvor hvert punkt i et plan er bestemt ut ifra avstanden fra et gitt punkt (vanligvis origo) og vinkel i forhold til X-aksen. I et vanlig kartesisk koordinatsystem blir punktene bestemt ut ifra avstanden til hver koordinatakse.

Prinsippet i polarkoordinater er at man angir alle punkter ved hjelp av følgende informasjon:

• Punktets vinkel (grader eller radianer ) i forhold til hva man ville kalle x-aksen i et rektangulært koordinatsystem, θ.
• Punktets avstand fra origo, r.

Konvertering mellom polare og kartesiske koordinater

Omregning polarkoordinater til kartesiske koordinater kan gjøres ved:

${\displaystyle x=r\cos \theta \,}$

${\displaystyle y=r\sin \theta ,\,}$

Mens omregningen fra karteiske koordinater til poolarkoordinater kan gjøres ved:

${\displaystyle r={\sqrt {y^{2}+x^{2}}}\quad }$ (Gitt ved Pythagoras’ læresetning), og

${\displaystyle \theta ={\begin{cases}0&{\mbox{hvis }}x=0{\mbox{ og }}y=0\\\arcsin({\frac {y}{r}})&{\mbox{hvis }}x\geq 0\\\arcsin({\frac {y}{r}})+\pi &{\mbox{hvis }}x<0\\\end{cases}}}$

Alle disse formlene forutsetter at referansepunktet for polarkoordinatsystemet er origo. Arcsinfunksjonen er den inverse funksjonen til sinusfunksjonen og gir en løsning i intervallet [−π/2,+π/2], så formelen for θ vil gi en løsning i intervallet [−π/2,+π/2]. Dersom man vil finne θ i intervallet [0, 2π) kan man også bruke:

${\displaystyle \theta ={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{hvis }}x>0{\mbox{ og }}y\geq 0\\\arctan({\frac {y}{x}})+2\pi &{\mbox{hvis }}x>0{\mbox{ og }}y<0\\\arctan({\frac {y}{x}})+\pi &{\mbox{hvis }}x<0\\{\frac {\pi }{2}}&{\mbox{hvis }}x=0{\mbox{ og }}y>0\\{\frac {3\pi }{2}}&{\mbox{hvis }}x=0{\mbox{ og }}y<0\\0&{\mbox{hvis }}x=0{\mbox{ og }}y=0\end{cases}}}$

Anvendelse av polarkoordinater

En ligning uttrykt i polarkoordinater er kjent som en polar ligning. Normalt er disse ligningene gitt ved å definere r som en funksjon av θ. Denne definisjonen gir visse fordeler i anvendelsen av polarkoordinater i forhold til hva man kan oppnå med rektangulære. Særlig fordelaktig er det å bruke polarkoordinater hvor det inngår noe sirkulært. Det enklest tenkelige eksempel er å fremstille en sirkel. Her er definisjonen av en sirkel med radius 1.

${\displaystyle \left.{\begin{matrix}x=r\cdot \cos \theta \\y=r\cdot \sin \theta \end{matrix}}\right\}\quad ,r=1\quad ,\quad \theta \in [0,2\pi ]}$

Lengden til det bevegelige punktet, settes altså konstant til å være lik én, som altså er avstanden fra origo til periferien. Deretter settes vinkelen til å variere mellom 0 og 2π eksklusiv (eller 0 og 360° i vinkler), hvor hele sirklen er med.

Arkimedisk spiral

En arkimedisk spiral er en spiral som ble oppdaget av Arkimedes, som kan forklares med polarkoordinater. Spiralen har formelen

${\displaystyle r(\theta )=a+b\theta .\,}$

Ved å forandre a vil spiralen skifte form, mens b er distansen mellom kurvene, som for en gitt spiral alltid er konstant. Den Arkimediske spiralen har to kurver, en for θ > 0 og en for θ < 0. De to kurvene starter i origo. Sett bort fra kjeglesnittene var denne kurven blant de første til å bli beskrevet. Kurven er også et godt eksempel på kurver som blir best beskrevet med polarkoordinater.

Polar rose

En polar rose er en matematisk kurve som ser ut som en blomst med kronblader, denne kan defineres som en enkel polar ligning.

${\displaystyle r(\theta )=a\cos(k\theta +\phi _{0})\,}$

For enhver konstant ${\displaystyle \phi _{0}}$ (Inkludert 0). Dersom k er et heltall vil disse ligningene gi kurver hvor «blomsten» har k kronblader når k er et oddetall og 2k kronblader når k er et partall. Dersom k er et rasjonalt tall, men ikke et heltall vil man også få frem en blomst hvor kronbladene overlapper hverandre. Her må imidlertid definisjonsintervallet for kurven være større enn [0, 2π) for at «blomsten» skal bli komplett. Merk at det er umulig å definere en kurve hvor man får ${\displaystyle 4n+2}$, hvor n er et heltall, kronblader. Variabelen a angir lengden på kronbladene.

Kjeglesnitt

Alle kjeglesnittene kan også uttrykkes ved hjelp av polarkoordinater gjennom formelen:

${\displaystyle r={p \over {1+e\cos \theta }}}$

Hvor e er eksentrisiteten og p er semi latus rectum

Derson e > 1, vil ligningen gi en hyperbel; e = 1 gir en parabel mens e < 1 gir oss en ellipse. Spesialtilfellet e = 0 vil gi en sirkel mad radius p.

Anvendelse i tre dimensjoner

Polarkoordinater kan også anvendes til bruk i tre dimensjoner. Kulekoordinater og sylinderkoordinater inneholder begge polarkoordinatplanet, utvidet med en ekstra akse. De er viktige eksempel på mer generelle, krumlinjete koordinater.

Sylinderkoordinater

Sylinderkoordinater systemet er en utvidelse av polarkoordinater med en ekstra z-akse, på samme måte som det kartesiske koordinatsytemet i tre dimensjoner. Den tredje koordinaten er vanligvis uttrykt med en h eller en z, som beskriver høyden til det øvre planet i sylinderen. Alle tre koordinatene blir da skrevet (r, θ, z).

Sammenhengen mellom de tre sylinderkoordinatene og de respektive kartesiske koordinatene blir

${\displaystyle {\begin{aligned}x&=r\,\cos \theta \\y&=r\,\sin \theta \\z&=z.\end{aligned}}}$

Kulekoordinater

Kulekoordinatsystemet er et koordinatsystem basert på polarkoordinater. Kulekoordinater skiller seg fra polarkoordinater ved at høyden fra xy-planet blir beskrevet av en vinkel φ fra z-aksen. Avstanden fra origo er ρ slik at radien i xy-planet blir r = ρ sinφ. Vinkelen φ varierer med en størrelsene 0°-180° eller 0-π radianer. De tre koordinatene blir da skrevet (ρ, θ, φ).

Sammenhengen mellom de tre kulekoordinatene og de respektive kartesiske koordinatene er dermed

${\displaystyle {\begin{aligned}x&=\rho \,\sin \varphi \,\cos \theta \\y&=\rho \,\sin \varphi \,\sin \theta \\z&=\rho \,\cos \varphi .\end{aligned}}}$

Betegnelsene for disse tre koordinatene varierer. I fysikk og mer praktiske anvendelser er det vanlig å bytte navnene til de to vinklene. Ofte blir også avstanden fra origo gitt ved r i stedet for ρ slik at de kartesiske koordinatene kan skrives som

${\displaystyle {\begin{aligned}x&=r\,\sin \theta \,\cos \varphi \\y&=r\,\sin \theta \,\sin \varphi \\z&=r\,\cos \theta .\end{aligned}}}$

Litteratur

• J. Mathews and R.L. Walker, Mathematical Methods of Physics, W.A. Benjamin, New York (1970). ISBN 0-8053-7002-1.
• M.L. Boas, Mathematical Methods in the Physical Sciences, John Wiley & Sons, New York (1983). ISBN 0-471-04409-1.