Apollóniusz-kör

Az Apollóniusz-kör azoknak a pontoknak a mértani helye a síkban, amelyeknek két adott ponttól mért távolságainak aránya adott (1-től különböző) pozitív szám. Fontos szerepe van a bipoláris koordináta-rendszerekben. Felfedezője, Pergai Apollóniosz görög matematikus után nevezték el. Nem összekeverendő a szintén róla elnevezett Apollóniusz köreivel.

Definíció

Az A és B ponthoz és a ${\displaystyle \lambda }$ számhoz tartozó Apollóniusz-kör azon P pontok halmaza, amelyekre ${\displaystyle {\frac {PA}{PB}}=\lambda }$ (ha ${\displaystyle \lambda =1}$, akkor ez ${\displaystyle AB}$ felezőmerőlegese, ami tekinthető egy olyan körnek, aminek végtelen távol van a középpontja).

Annak bizonyítása, hogy a pontok kört alkotnak

• 1. lépés:

Legyen ${\displaystyle P}$ egy olyan pont, amely nincs rajta ${\displaystyle AB}$ egyenesén, és amelyre ${\displaystyle {\frac {PA}{PB}}=\lambda }$. Feltehetjük, hogy ${\displaystyle PA>PB}$ (ekkor ${\displaystyle \lambda >1}$). ${\displaystyle PAB}$ háromszögnek ${\displaystyle P}$-ből induló belső szögfelezője az ${\displaystyle AB}$ oldalt egy ${\displaystyle C}$ pontban metszi, külső szögfelezője pedig ${\displaystyle \lambda >1}$ miatt ${\displaystyle AB}$-nek ${\displaystyle B}$-ből induló meghosszabbítását metszi ${\displaystyle D}$-ben.

Segédtétel:

Ha egy háromszög egyik oldalának az egyenesét a szemközti csúcsból induló (belső vagy külső) szögfelezővel metsszük, akkor a metszéspontnak az oldal végpontjaitól mért távolságai úgy aránylanak egymáshoz, mint a szemközti csúcsból ehhez a végpontokhoz vezető oldalak.

Emiatt ${\displaystyle C}$ és ${\displaystyle D}$ a keresett mértani helyhez tartozik.

• 2. lépés:

Be kell látni, hogy a mértani helyek minden ${\displaystyle P}$ pontja ugyanezen a körön van, ehhez elég megmutatni, hogy az ${\displaystyle AB}$ egyenes pontjai közül csak ${\displaystyle C}$ és ${\displaystyle D}$ tartozik a mértani helyhez. A szögfelezők merőlegesek egymásra, ezért ${\displaystyle P}$ a ${\displaystyle CD}$ távolság Thalész-körén van. ${\displaystyle \lambda >1}$ miatt elég, hogy sem az ${\displaystyle AB}$ szakaszon, sem a ${\displaystyle BD}$ félegyenesen nincs más, a mértani helyhez tartozó pont. Ha ${\displaystyle C}$ az ${\displaystyle AB}$ távolságon ${\displaystyle B}$ felé mozog, akkor az ${\displaystyle {\frac {AC}{CB}}}$ arány nő. Ha ${\displaystyle D}$ a ${\displaystyle BD}$ félegyenesen ${\displaystyle B}$-ből kiindulva mozog, akkor a ${\displaystyle {\frac {AD}{DB}}}$ arány csökken, ugyanez a helyzet, ha ${\displaystyle D}$ távolodik ${\displaystyle B}$-től. Más szóval ${\displaystyle C}$ és ${\displaystyle D}$ helyzete egyértelműen meghatározott, vagyis a keresett mértani hely minden pontja a ${\displaystyle CD}$ szakasz Thalész-körén van.

• 3. lépés:

Be kell bizonyítani, hogy ennek a körnek minden pontja a mértani helyhez tartozik (${\displaystyle C,D}$ pontokról tudjuk ezt). Legyen ${\displaystyle P}$ a körnek egy további pontja. Elég belátni, hogy ${\displaystyle PC}$ és ${\displaystyle PD}$ a ${\displaystyle PAB}$ háromszög szögfelezői, ekkor ${\displaystyle {\frac {PA}{PB}}={\frac {CA}{CB}}=\lambda }$. Ehhez indirekt tegyük fel, hogy ${\displaystyle PAB}$ háromszög szögfelezői ${\displaystyle PC^{*}}$ és ${\displaystyle PD^{*}}$, ami nem azonos a ${\displaystyle PC}$ és ${\displaystyle PD}$ egyenesekkel. ${\displaystyle C}$ és ${\displaystyle D}$ választása miatt ${\displaystyle {\frac {AC}{CB}}={\frac {AD}{DB}}}$ és ${\displaystyle {\frac {AC^{*}}{C^{*}B}}={\frac {AD^{*}}{D^{*}B}}}$. 1) miatt ez csak úgy lehet, ha vagy ${\displaystyle CD}$ tartalmazza ${\displaystyle C^{*}D^{*}}$ távolságot, vagy fordítva. Ekkor viszont ${\displaystyle CPD}$ szög és ${\displaystyle C^{*}PD^{*}}$ szög közül az egyik tartalmazza a másikat. Ezzel ellentmondáshoz jutottunk, mivel mindkét szög derékszög (Thalész-tétel vagy a szögfelezők merőlegessége miatt). Tehát ${\displaystyle PC,PD}$ szögfelezők, ekkor ${\displaystyle CD}$ Thalész-körének minden pontja a mértani helyhez tartozik.

Tulajdonságai

• A λ arányhoz tartozó Apollóniusz-kör sugara ${\displaystyle r_{A}={\frac {\lambda }{|\lambda ^{2}-1|}}{\overline {AB}}}$.
• Ha egy Apollóniusz-körre vonatkozó inverzióban A és B egymásba megy át, akkor ebben az inverzióban az összes A-n és B-n átmenő kör önmagába megy át. Ezért minden ilyen kör merőlegesen metszi az összes Apollóniusz-kört.
• Tekintsük most a K Apollóniusz-kört annak egy tetszőleges X pontjával, és az AXB szög szögfelezői által a K körből kimetszett T₁ és T₂ pontokkal. Jelölje továbbá λ a K-hoz tartozó arányt. Ekkor a harmonikus elválasztás kölcsönössége miatt az AB szakaszon átmenő kör a T₁T₂ szakasz Apollóniusz-köre lesz.
• Az előző állítás jelöléseivel: a K kör éppen az a T₁-en és T₂-n átmenő kör, amire A és B inverz pontpárok.

Kapcsolat a projektív geometriával

A sík körei természetes módon megfeleltethetők a háromdimenziós projektív tér pontjainak. Ebben a megfeleltetésben a projektív egyenesek képei a körsorok. Speciálisan, az Apollóniusz-körök és a két ponton átmenő körök is egy-egy körsort alkotnak.

Például a (p,q) középpontú, r sugarú kör egyenlete:

${\displaystyle \displaystyle (x-p)^{2}+(y-q)^{2}=r^{2},}$

átírható az

${\displaystyle \displaystyle \alpha (x^{2}+y^{2})-2\beta x-2\gamma y+\delta =0,}$

alakba, ahol α = 1, β = p, γ = q, and δ = p² + q² − r². Ez a négy paraméter azonban csak egy skalár erejéig meghatározott, ugyanis ha végigszorozzuk őket egy nem nulla számmal, akkor ugyanazt a kört kapjuk. Így ezek az együtthatók a kör homogén koordinátáinak tekinthetők a körök háromdimenziós projektív terében.^[1] Ha α = 0, akkor a kör egyenessé fajul el. Ha α ≠ 0, akkor visszajutunk a kör egyenletéhez a p = β/α, q = γ/α, és az r =√((−δ − β ² − γ²)/α²) együtthatókkal. Itt előfordulhat, hogy a gyökjel alá egy nem pozitív szám kerül; ebben az esetben nullkört, vagy képzetes kört ír le az egyenlet.

Két kör, (α₁,β₁,γ₁,δ₁) és (α₂,β₂,γ₂,δ₂) affin kombinációja a :${\displaystyle \displaystyle z(\alpha _{1},\beta _{1},\gamma _{1},\delta _{1})+(1-z)(\alpha _{2},\beta _{2},\gamma _{2},\delta _{2})}$ négyest adja, ahol z szabadon változhat. Ez a két kör által generált körsor. Háromféle körsort különböztetünk meg a körsor generátorainak közös pontjainak száma szerint: az elliptikust, a parabolikust és a hiperbolikust.^[2] Valójában a hiperbolikus körsor két pontkört és képzetes köröket is tartalmaz. A két pontkör a körsor Poncelet-pontjai. Az Apollóniusz-körök is ilyen körsort adnak. A koncentrikus körök hiperbolikus körsorának is két tartópontja van: a másik tartópont a végtelenben van. Az erre merőleges körök körsora a két tartópontot összekötő körök, valójában egyenesek körsora.

Inverzió és koordináta-rendszerek

Az inverziók a körsorokat körsorokba viszik, sőt a típusukat is megtartják, így elliptikus körsor képe elliptikus, parabolikus körsor képe parabolikus, hiperbolikus körsor képe hiperbolikus lesz.

Egy A közepű körre vonatkozó inverzió az Apollóniusz-köröket B középpontú koncentrikus körökbe viszi. Ugyanez az inverzió az A-n és a B-n átmenő köröket a B-n átmenő egyenesekbe transzformálja. Így az Apollóniusz-körök által meghatározott két pólusú koordináta-rendszer polár-koordinátarendszerbe megy át.

Általánosabban, minden körsorhoz van egy egyértelmű hozzá ortogonális körsor. Hiperbolikus körsor ortogonális körsora elliptikus, elliptikus körsor ortogonális körsora hiperbolikus, és parabolikus körsor ortogonális körsora parabolikus. A hiperbolikus körsor ortogonális körsora a Poncelet-pontjain átmenő körök alkotta körsor; elliptikus körsor ortogonális körsora a közös metszéspontok Apollóniusz-köreiből áll; parabolikus körsor ortogonális körsora a vele azonos érintési pontú, de merőleges tengelyű körsor.

Jegyzetek

Fordítás

Ez a szócikk részben vagy egészben a Kreis des Apollonios című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként. Ez a szócikk részben vagy egészben az Apollonian circles című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Források

• http://www.herder-oberschule.de/madincea/aufg0009/harmonie.pdf

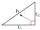Ez a geometriai témájú lap egyelőre csonk (erősen hiányos). Segíts te is, hogy igazi szócikk lehessen belőle!