Distribución de Erlang

Distribución de Erlang
Función de densidad de probabilidad
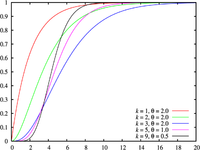Función de distribución de probabilidad
Parámetros	${\displaystyle n\in \mathbb {Z} ^{+}}$ ${\displaystyle \lambda >0\,}$
Dominio	${\displaystyle [0,\infty )\!}$
Función de densidad (pdf)	${\displaystyle {\frac {\lambda (\lambda x)^{n-1}e^{-\lambda x}}{(n-1)!}}}$
Función de distribución (cdf)	${\displaystyle 1-\sum _{k=0}^{n-1}{\frac {(\lambda x)^{k}e^{-\lambda x}}{k!}}}$
Media	${\displaystyle {\frac {n}{\lambda }}}$
Mediana	—
Moda	${\displaystyle {\frac {n-1}{\lambda }}}$ para ${\displaystyle n\geq 1}$
Varianza	${\displaystyle {\frac {n}{\lambda ^{2}}}}$
Coeficiente de simetría	${\displaystyle {\frac {2}{\sqrt {n}}}}$
Curtosis	${\displaystyle {\frac {6}{n}}}$
Entropía	${\displaystyle (1-n)\psi (n)+\ln {\frac {\Gamma (n)}{\lambda }}+n}$
Función generadora de momentos (mgf)	${\displaystyle \left({\frac {\lambda }{\lambda -t}}\right)^{n}\,}$ para ${\displaystyle t<\lambda }$
Función característica	${\displaystyle \left({\frac {\lambda }{\lambda -it}}\right)^{n}}$
[editar datos en Wikidata]

En la teoría de la probabilidad y estadística, la distribución Erlang es una distribución de probabilidad continua con dos parámetros dados por

• ${\displaystyle n}$ el factor de forma de la distribución.
• ${\displaystyle \lambda }$ el factor de proporción de la distribución.

Definición

Función de Densidad

Una variable aleatoria continua ${\displaystyle X}$ tiene distribución de Erlang con parámetros ${\displaystyle n\in \mathbb {Z} ^{+}}$ y ${\displaystyle \lambda >0}$ y escribimos ${\displaystyle X\sim \operatorname {Erlang} (n,\lambda )}$ si la función de densidad para valores ${\displaystyle x>0}$ es

${\displaystyle f(x)={\frac {\lambda (\lambda x)^{n-1}e^{-\lambda x}}{(n-1)!}}}$

Esta distribución se utiliza para describir el tiempo de espera hasta el suceso número ${\displaystyle n}$ en un proceso de Poisson.

Esta distribución recibe su nombre en honor al matemático e ingeniero danés Agner Krarup Erlang, quien la introdujo en 1909 para examinar el número de llamadas telefónicas que pueden asignarse simultáneamente a las operadoras de conmutadores. Este trabajo de ingeniería de tráfico telefónico se ha ampliado para considerar los tiempos de espera en los sistemas de colas en general. La distribución también se utiliza en el campo de los procesos estocásticos.

Función de Distribución

Si ${\displaystyle X\sim \operatorname {Erlang} (n,\lambda )}$ entonces su función de distribución acumulada está dada por

${\displaystyle {\begin{aligned}F(x)&=\sum _{k=n}^{\infty }{\frac {(\lambda x)^{k}e^{-\lambda x}}{k!}}\\&=1-\sum _{k=0}^{n-1}{\frac {(\lambda x)^{k}e^{-\lambda x}}{k!}}\end{aligned}}}$

Propiedades

Si ${\displaystyle X\sim \operatorname {Erlang} (n,\lambda )}$ entonces

• La esperanza de la variable aleatoria ${\displaystyle X}$ es

${\displaystyle \operatorname {E} [X]={\frac {n}{\lambda }}}$

• La varianza de la variable aleatoria ${\displaystyle X}$ es

${\displaystyle \operatorname {Var} (X)={\frac {n}{\lambda ^{2}}}}$

• La función generadora de momentos está dada por

${\displaystyle M_{X}(t)=\left({\frac {\lambda }{\lambda -t}}\right)^{n}}$

Distribuciones Relacionadas

• La distribución de Erlang es un caso particular de la distribución Gamma pues si ${\displaystyle X\sim \Gamma (\alpha ,\lambda )}$ con ${\displaystyle \alpha =n\in \mathbb {N} }$ entonces ${\displaystyle X\sim \operatorname {Erlang} (n,\lambda )}$.
• Si ${\displaystyle X\sim \operatorname {Erlang} (1,\lambda )}$ entonces ${\displaystyle X\sim \operatorname {Exponencial} (\lambda )}$.

Aplicaciones

Tiempos de espera

La implementación original del modelo de distribución se dio en el área de la telefonía en grandes concentraciones. En este caso, los eventos que ocurren independientemente con una tasa promedio se modelan con un proceso de Poisson. Los tiempos de espera entre k ocurrencias del evento se distribuyen en un Erlang. (Como factor relevante relacionado, el número de eventos en un período de tiempo determinado se describe mediante la distribución de Poisson)

La distribución Erlang, cuando es usada para medir el tiempo entre llamadas entrantes, se puede utilizar junto con la duración esperada de las mismas para producir información sobre la carga de tráfico medida en erlangs. Esto se puede usar para determinar la probabilidad de pérdida o retraso de eventos (en telefonía abandono o espera prolongada), de acuerdo con varias suposiciones sobre si las llamadas bloqueadas se abortan (fórmula Erlang B) o se ponen en cola de espera hasta que ser atendidas (fórmula Erlang C). Las fórmulas de Erlang-B y C todavía se usan a diario para el modelado de tráfico para aplicaciones como el diseño de centros de llamadas.

Otras aplicaciones

La incidencia de cáncer, distribuida por edad, a menudo sigue la distribución de Erlang, mientras que los parámetros de forma y escala predicen, respectivamente, la cantidad de eventos causales y el intervalo de tiempo entre ellos.^[1]​^[2]​ De manera más general, la distribución de Erlang se ha sugerido como una buena aproximación de la distribución del tiempo del ciclo celular, como resultado de modelos de múltiples etapas.^[3]​^[4]​

También se ha utilizado en economía empresarial para describir tiempos entre compras.^[5]​

Véase también

• Distribución gamma
• Distribución exponencial
• Distribución beta
• Distribución normal
• Proceso de Poisson

Referencias

Enlaces externos

• Calculadora Distribución de Erlang